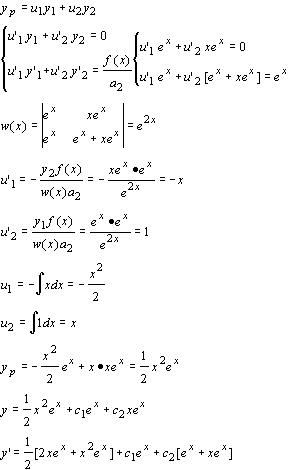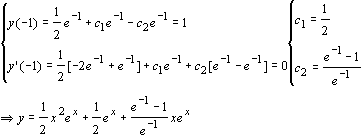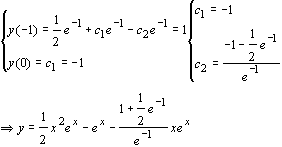CAPITOLO 1
SVOLGIMENTO
EQUAZIONI DIFFERENZIALI
IL METODO DEGLI ANNICHILATORI
Il metodo può essere usato se l’equazione L(y)=R ha coefficienti costanti e se il secondo membro R è annichilato esso stesso da un operatore a coefficienti costanti, cioè A(R)=0. Applichiamo l’operatore ad entrambi i membri dell’equazione differenziale L(y)=R , otteniamo una nuova equazione AL(y)=0 che deve essere soddisfatta da tutte le soluzioni dell’equazione data. Poichè AL è un altro operatore a coefficienti costanti possiamo determinare il suo nucleo calcolando le radici dell’equazione caratteristica. Allora il problema si riduce a quello di scegliere in questo nucleo una funzione particolare y1 che soddisfi L(y1)=R.
Elenchiamo questi annichilatori:
funzione Annichilatore
y=xm-1 Dm
y=ea x D-a
y= xm-1 ea x (D-a )m
y=cos b x oppure y=sin b x D2-b 2
y= xm-1 cos b x oppure y=xm-1 sin b x (D2-b 2)m
y= ea x cos b x oppure y= ea x sin b x D2-2a D+(a 2+b 2)
y= xm-1 ea x cos b x oppure y= xm-1 ea x sin b x [D2-2a D+(a 2+b 2)]m
Esercizio n. 1.1 -
Il polinomio caratteristico è :
pA(r) = 5r2 + 4r + 1
le radici del quale sono:
![]()
![]()
allora la soluzione generale è: x(t) = e-(2/5)t[c1 cos(1/5)t + c2 sin(1/5)t]
Esercizio n. 1.2-
Il polinomio caratteristico è:
pA(r) = r2 - 4r + 3
le radici del quale sono:
![]()
cioè: 3,1
Quindi la soluzione generale dell’ equazione omogenea è:
x(t)=c1 e3t + c2 et
Ora:
x(0) = c1 + c2 = 6
x’(t) = 3c1 e3t + c2 et
x’(0) = 3c1 + c2 = 10
ne risulta il seguente sistema:
c1 + c2 = 6
3c1 + c2 = 10
che risolto da come risultato:
c1 = 2 c2 =4
la soluzione del problema di Cauchy e: x(t) = 2 e3t + 4 et
Esercizio n. 1.3-
Il polinomio caratteristico è:
pA(r) = 3r2 - 5r - 2
le radici del quale sono:
![]()
cioè:2,-1/3
Quindi la soluzione generale dell’ equazione omogenea è:
x(t)=c1 e2t + c2 e-(1/3)t
Ora:
x(0) = c1 + c2 = 1
x’(t) = 2c1 e2t - (1/3)c2 e-(1/3)t
x’(0) = 2c1 - (1/3)c2 = 1
ne risulta il seguente sistema:
c1 + c2 = 1
2c1 - (1/3)c2 = 1
che risolto da come risultato:
c1 = 4/7 c2 = 3/7
la soluzione del problema di Cauchy e: x(t) = (4/7) e2t + (3/7) e-(1/3)t
Esercizio n. 1.4-
a)Il polinomio caratteristico è :
pA(r) = r2 + 2r + 5
le radici del quale sono:
![]()
allora la soluzione generale è: y(t) = e-t[c1 cos2t + c2 sin2t]
b) Il polinomio caratteristico è:
pA(r) = r2 + 4r + 4
le radici del quale sono:
![]()
cioè:2 di molteplicità 2
Quindi la soluzione generale è: y(t)=c1 e-2t + c2 te-2t
c) Il polinomio caratteristico è:
pA(r) = r2 - 4r - 12
le radici del quale sono:
![]()
Quindi la soluzione generale è: y(t)=![]()
Esercizio n. 1.5-
L’ equazione omogenea associata si può scrivere come:
(D2 + 2D -8)y = 0 che si può scomporre in: (D-2)(D+4)y = 0
questa equazione ha le soluzioni indipendenti u1(x) = e2x , u2(x) = e-4x
Cerchiamo ora una soluzione particolare della equazione non omogenea.
Osserviamo che R(x) = -8x2 + 4x - 14 è una soluzione dell’equazione D3y = 0 e questo è l’annichilatore.
Infatti
R’(x) = -16x +4
R’’(x) = -16
R’’’(x) = 0
D3(-8x2 + 4x - 14) = 0
Perciò se si applica ad entrambi i membri dell’equazione non omogenea l’operatore D3 si trova che ogni funzione che soddisfa la non omogenea deve anche soddisfare l’equazione:
D3(D-2)(D+4)y = 0
l’operatore D3 contiene le funzioni indipendenti: u1(x) = 1 , u2(x) = x, u3(x) =x2
considero quindi y1 = A + Bx + C x2
senza le soluzioni dell’omogenea poiché (D-2)(D+4)(c1 e2x + c2 e-4x) = 0
si ha: D(y1) = 2Cx + B
D2(y1) = 2C
cosicché l’equazione (D2 + 2D -8)y = -8x2 + 4x - 14 diventa:
2C + 2(2Cx + B) - 8(A + Bx + C x2) = -8x2 + 4x - 14
uguagliando i coefficienti a destra e sinistra otteniamo il seguente sistema:
2C - 8A = -14
4C - 8B = 4
-8C = -8
quindi A = 2, B = 0, C = 1
la soluzione generale dell’equazione non omogenea è:
y(x) = c1 e2x + c2 e-4x + 2 + x2
utilizzando ora le condizioni iniziali troviamo i valori di c1 , c2 .
y(0) = c1 + c2 + 2 = 7
y’(x) = 2c1 e2x - 4c2 e-4x + 2x
y’(0) = 2c1 - 4c2 = -8
dobbiamo risolvere quindi il sistema:
c1 + c2 + 2 = 7
2c1 - 4c2 = -8
le soluzioni sono c1 = 2 ,c2 = 3
la soluzione generale del problema di Cauchy è quindi:
y(x) = 2e2x + 3e-4x + 2 + x2
Esercizio n. 1.6-
L’equazione omogenea associata si può scrivere come:
(D2 + 8D +7)y = 0 che si può scomporre in: (D+7)(D+1)y = 0
questa equazione ha le soluzioni indipendenti u1(x) = e-7x , u2(x) = e-x
Cerchiamo ora una soluzione particolare della equazione non omogenea.
Osserviamo che R(x) = (x+4)cos3x è una soluzione dell’equazione
(D2 + 32)2 = 0 che scomposto è : (D2 + 32) (D2 + 32)y = 0 e questo è l’annichilatore.
Infatti R’(x) = cos3x - 3(x+4)sin3x
R’’(x) = -3sin3x- 3[sin 3x + 3(x+4)cos3x]
= -6sin3x - 9(x+4)cos3x
(D2 + 32)(-6sin3x) = 0 infatti D = -18cos3x, D2 = 54sin3x e
54sin3x + 9(-6sin3x) = 0
Perciò se si applica ad entrambi i membri dell’equazione non omogenea l’operatore (D2 + 32)2 si trova che ogni funzione che soddisfa la non omogenea deve anche soddisfare l’equazione:
(D2 + 32)2(D+7)(D+1)y = 0
l’operatore (D2 + 32)2 contiene le funzioni indipendenti:
u1(x) = cos3x, u2(x) = xcos3x
v1(x) = sin 3x, v2(x) = xsin3x
considero allora: y1 = (A + Bx)cos3x + (C + Dx)sin3x
si ha:
D(y1) = Bcos3x - 3(A + Bx)sin3x + Dsin3x + 3(C + Dx)cos3x
=(D-3A-3Bx)sin3x + (B+3C+3Dx)cos3x
D2(y1) = -3Bsin3x+3(D-3A-3Bx)cos3x+3Dcos3x-3(B+3C+3Dx)sin3x
=(6D-9A-9Bx)cos3x - (6B+9C+9Dx)sin3x
cosicché l’equazione (D2 + 8D +7)y1 = (x+4)cos3x diventa:
(6D-9A-9Bx)cos3x-(6B+9C+9Dx)sin3x+8[(D-3A-3Bx)sin3x+(B+3C+3Dx)cos3x]+ +7[(A+Bx)cos3x+(C+Dx)sin3x]=(x+4)cos3x
possiamo uguagliare i coefficienti del seno e del coseno risulta:
-(6B+9C+9Dx)+8(D-3A-3Bx)+7(C+Dx) = 0
quindi:-24A-6B-2C+8D-24Bx-2Dx = 0
(6D-9A-9Bx)+8(B+3C+3Dx)+7(A+Bx) = x+4
quindi: -2A+8B+24C-2Bx+24Dx = x+4
dalle quali possiamo scrivere il sistema:
-24A-6B-2C+8D = 0
-24B-2D = 0
-2A+8B+24C = 4
-2B+24D = 1
le soluzioni del quale sono:
A = 562/21025
B = - 1/290
C= -6093/42050
D = 6/145
La soluzione generale dell’equazione non omogenea è:
y(x) = c1 e-7x + c2 e-x + (A+Bx)cos3x + (C+Dx)sin3x
Ora y(-1) = 1 e y’(-1) = 0
y’(x) = -7c1 e-7x - c2 e-x + Bcos3x - 3(A+Bx)sin3x + Dsin3x + 3(C+Dx)cos3x
= -7c1 e-7x - c2 e-x + (D-3A-3Bx)sin3x + (B+3C+3Dx)cos3x
si ottiene quindi il sistema:
y(-1) = c1 e7 + c2 e + (A-B)cos3 - (C-D)sin3 = 1
y’(-1) = -7c1 e7 - c2 e - (D-3A+3B)sin3 + (B+3C-3D)cos3=0
risolto per sostituzione dà:
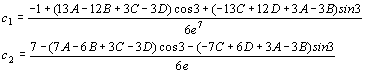
sostituendo A,B,C,D trovati prima troviamo le due costanti c1,c2
e quindi la soluzione generale del problema di Cauchy.
Esercizio n. 1.7-
L’equazione omogenea associata si può scrivere come
(3D2 + 10D +3)y = 0 che si può scomporre in: (D+3)(D+1/3)y = 0
questa equazione ha le soluzioni indipendenti u1(x) = e-3x , u2(x) = e-(1/3)x
Cerchiamo ora una soluzione particolare della equazione non omogenea.
Osserviamo che R(x) = (x+4)ex è una soluzione dell’equazione
(D - 1)2 = 0 che scomposto è : (D - 1) (D - 1)y = 0 e questo è l’annichilatore.
Infatti
R’(x) = ex + (x+4)ex
(D-1)( ex )=0 infatti D(ex)= ex ed ex - ex = 0
Perciò se si applica ad entrambi i membri dell’equazione non omogenea l’operatore (D - 1)2 si trova che ogni funzione che soddisfa la non omogenea deve anche soddisfare l’equazione:
(D - 1)2(D+3)(D+1/3)y = 0
l’operatore (D - 1)2 contiene le funzioni indipendenti:
u1(x) = ex , u2(x) = x ex
allora considero y1 = (A+Bx) ex
senza le soluzioni dell’omogenea poichè
(D+3)(D+1/3)( c1e-3x + c2e-(1/3)x ) = 0
D(y1) = Bex + (A+Bx) ex = (A+B+Bx) ex
D2(y1) = Bex + Bex + (A+Bx) ex = (A+2B+Bx) ex
cosicchè l’equazione (3D2 + 10D +3)y1 = (x+4)ex diventa
3(A+2B+Bx) ex + 10(A+B+Bx) ex + 3(A+Bx) ex = (x+4)ex
uguagliando i coefficienti dell’esponenziale si ha
16A+16B+16Bx = x+4 dalla quale otteniamo il seguente sistema
16A+16B = 4
16B = 1
le soluzioni sono: A=3/16,B=1/16
la soluzione generale della non omogenea è:
y(x)= c1e-3x + c2e-(1/3)x + (A+Bx) ex
per trovare c1 e c2 utilizziamo le condizioni iniziali
y(-1) = 0, y’(-1) = 0
y’(x)= -3c1e-3x -(1/3)c2e-(1/3)x + Bex +(A+Bx) ex
quindi otteniamo il seguente sistema
y(-1) = c1e3 + c2e(1/3) + (A-B) e-1 = 0
y’(-1) = -3c1e3 -(1/3)c2e(1/3) + Bex +(A-B) e-1 = -3c1e3 -(1/3)c2e(1/3) + Ae-1
che risolto per sostituzione da come risultato
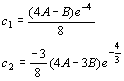
sostituendo i valori di A e B si trovano le costanti e quindi la soluzione generale del problema di Cauchy.
Esercizio n. 1.8-
L’equazione omogenea associata si può scrivere come
(D2 + 2D + 1)y = 0 che si può scomporre in: (D+1)2y = 0
questa equazione ha le soluzioni indipendenti u1(x) = e-x , u2(x) = xe-x
Cerchiamo ora una soluzione particolare della equazione non omogenea.
Osserviamo che R(x) = xex è una soluzione dell’equazione
(D - 1)2 = 0 che scomposto è : (D - 1) (D - 1)y = 0 e questo è l’annichilatore.
Infatti
R’(x) = ex + xex
(D-1)( ex )=0 infatti D(ex)= ex ed ex - ex = 0
Perciò se si applica ad entrambi i membri dell’equazione non omogenea l’operatore (D - 1)2 si trova che ogni funzione che soddisfa la non omogenea deve anche soddisfare l’equazione:
(D - 1)2(D+1)2y = 0
l’operatore (D - 1)2 contiene le funzioni indipendenti:
u1(x) = ex , u2(x) = x ex
allora considero y1 = (A+Bx) ex
senza le soluzioni dell’omogenea poichè
(D+1)2( c1e-x + c2xe-x ) = 0
D(y1) = Bex + (A+Bx) ex = (A+B+Bx) ex
D2(y1) = Bex + Bex + (A+Bx) ex = (A+2B+Bx) ex
cosicchè l’equazione (D2 + 2D +1)y1 = xex diventa
[(A+2B+Bx) ex]+2[(A+B+Bx) ex]+ (A+Bx) ex = xex
dal quale uguagliando i coefficienti a destra e sinistra otteniamo il seguente sistema
4A+4B = 0
4B = 1
che dà come soluzioni A=-(1/4), B=1/4
la soluzione generale è data da: y(x)= c1e-x + c2xe-x + [-(1/4)+(1/4)x] ex
le costanti le troviamo dalle condizioni iniziali
y’(x) = -c1e-x + c2e-x - c2xe-x + (1/4)ex + [-(1/4)+(1/4)x] ex
dalle quali troviamo il seguente sistema
y(-1) = c1e - c2e + [-(1/4)-(1/4)] e-1 = c1e - c2e -(1/2)e-1 = 0
y’(1) = -c1e-1 + c2e-1 - c2e-1 + (1/4)e1 + [-(1/4)+(1/4)] e1 = -c1e-1 + (1/4)e1 = 0
dalle quali per sostituzione troviamo
c1 = (1/4)e2
c2 = -(1/2)e-2 + (1/4)e2
troviamo cosi la soluzione generale del problema di Cauchy.
Esercizio n. 1.9-
ydy = xdx allora integrando entrambi i membri si ha che ![]() ovvero y2 - x2 = C1 dove C1 = 2C è una costante arbitraria. Le curve delle soluzioni sono le iperboli equilatere con asinoti y = x e y = -x.
ovvero y2 - x2 = C1 dove C1 = 2C è una costante arbitraria. Le curve delle soluzioni sono le iperboli equilatere con asinoti y = x e y = -x.
Esercizio n. 1.10-
![]()
poichè y=3 quando x = 1 (è dato dal problema) si ha che ![]() . Sostituendo questo valore nella soluzione appena scritta e risolvendo rispetto a y otteniamo:
. Sostituendo questo valore nella soluzione appena scritta e risolvendo rispetto a y otteniamo: ![]() . Questa soluzione è valida per
. Questa soluzione è valida per 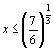
Esercizio n. 1.11-
Dobbiamo determinare m
(x) soluzione dell’equazione differenziale ![]() allora m
(x) = ln x allora em
(x) = x.
allora m
(x) = ln x allora em
(x) = x.
Allora calcoliamo ![]() e mediante integrazione
e mediante integrazione ![]() . Questa funzione è soluzione dell’equazione considerata per qualunque valore della costante C.
. Questa funzione è soluzione dell’equazione considerata per qualunque valore della costante C.
Esercizio n. 1.12-
p(x) = x allora m (x) = x2/2
![]() Calcoliamo
Calcoliamo
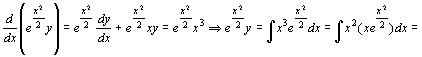
![]()
poichè
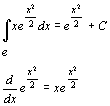
Quindi ![]()
Esercizio n. 1.13-
L’equazione è omogenea. Posto y = vx si ha che ![]()
allora ![]()
posto u = 1 - v2 si ha du = -2vdv e quindi ![]()
dove C1 = ln C. Allora ![]() dove C2 = 1/C1.
dove C2 = 1/C1.
Allora ![]() ed è il modo migliore per esprimere la soluzione.
ed è il modo migliore per esprimere la soluzione.
Esercizio n. 1.14-
L’equazione ausiliaria è r2 + r -2 = 0. Allora (r + 2)(r - 1) =0 e le radici sono: r1 = -2, r2 = 1. Quindi la soluzione generale è y(t) = A e-2t + B et .
Esercizio n. 1.15-
L’equazione ausiliaria è r2 + 6r + 9 = 0. Allora (r+3)2 = 0 che ha radici coincidenti r = -3. Allora la soluzione generale è y(t) = A e-3t + Bt e-3t
Esercizio n. 1.16-
L’equazione ausiliaria è r2 + 4r + 13 = 0. Il discriminante è D = b2 - 4ac = 16 - 52 = - 36 < 0.Abbiamo parte reale - (b/2a) = - 2 e parte immaginaria w
= ![]() = 3. Per cui la soluzione generale dell’equazione differenziale data è: y(t) = A e-2t cos 3t+ B e-2t sin 3t.
= 3. Per cui la soluzione generale dell’equazione differenziale data è: y(t) = A e-2t cos 3t+ B e-2t sin 3t.
Esercizio n. 1.17-
Abbiamo b2 - 4ac = 4 - 8 = -4 <0 . Inoltre parte reale - (b/2a) = - 1 e parte immaginaria w
= ![]() = 1. Quindi la soluzione generale dell’equazione differenziale data è : y(t) = A e-t cos t+ B e-t sin t.
= 1. Quindi la soluzione generale dell’equazione differenziale data è : y(t) = A e-t cos t+ B e-t sin t.
Inoltre risulta:
y’(t) = e-t ( - A cos t - B sin t -A sin t + B cos t) = (B-A) e-t cos t - (A+B) e-t sin t .
Imponendo le condizioni iniziali:
y(0) = 2. Allora A = 2
y’(0) = -3. Allora B-A = -3. Pertanto B = -1.
La soluzione del problema di Cauchy è: y(t) = 2 e-t cos t - e-t sin t
Esercizio n. 1.18-
Risolviamo dapprima l’equazione omogenea y’’ - 3y’ + 2y = 0. Questa ha equazione ausiliaria r
2 - 3r + 2 = 0, cioè (r - 1)(r - 2) = 0 quindi con radici r1 = 1 e r2 = 2. Pertanto le due soluzioni indipendenti dell’equazione omogenea sono y1 (x) = ex e y2 (x) = e2x e la funzione complementare è y0 (x) = C1 ex + C2 e2x (che è la soluzione generale dell’equazione omogenea).Una soluzione particolare yp (x) dell’ equazione non omogenea può essere determinata nella forma:
yp (x) = [u1 (x)] ex + [u2 (x)] e2x
dove u1 (x) e u2 (x) soddisfano il sistema di due equazioni:
[u’1 (x)] ex + [u’2 (x)] e2x = 0
[u’1 (x)] ex + 2[u’2 (x)] e2x = 4x
Il wronskiano del sistema è:
![]()
Quindi
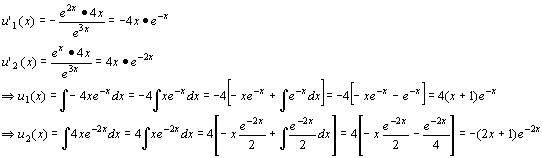
Quindi
![]()
La soluzione generale della non omogenea è quindi:
y(x) = yp (x) + y0 (x) = 2x + 3 + C1 ex + C2 e2x.
Esercizio n. 1.19-
y’’+4y = 0 Allora r2 + 4 = 0, D = -16 < 0 Allora la parte reale è -(b/2a) = 0 e la parte immaginaria w
= ![]() = 2.
= 2.
Allora la soluzione generale della omogenea è: y(x) = A cos 2x + B sin 2x
Allora y0 (x) = A cos 2x + B sin 2x
Poniamo yp (x) = [u1 (x)] cos 2x + [u2 (x)] sin 2x
Considero il sistema di due equazioni:
[u’1 (x)] cos 2x + [u’2 (x)] sin 2x = 0
-2[u’1 (x)] sin 2x + 2[u2 (x)] cos 2x = sin x
Il wronskiano è:
![]()
![]()
![]()
![]()
![]()
![]()

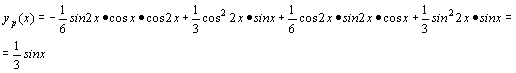
Quindi la soluzione generale dell’equazione non omogenea è:
y(x) = (1/3)sinx + A cos 2x + B sin 2x
Esercizio n. 1.20-
y’’ + 2y’ -8y = 0 Allora r2 + 2r -8 = 0 Allora r1,2 =![]() Allora r1 = 2, r2 = -4.
Allora r1 = 2, r2 = -4.
Quindi y0 (x) = C1 e2x + C2 e-4x e yp (x) =[ u1 (x)]e2x + [u2 (x)]e-4x
Consideriamo quindi il sistema di due equazioni
[ u’1 (x)]e2x + [u’2 (x)]e-4x = 0
2[ u’1 (x)]e2x -4 [u’2 (x)]e-4x = -8x2 +4x -14
Il wronskiano è:
![]()
![]()
![]()
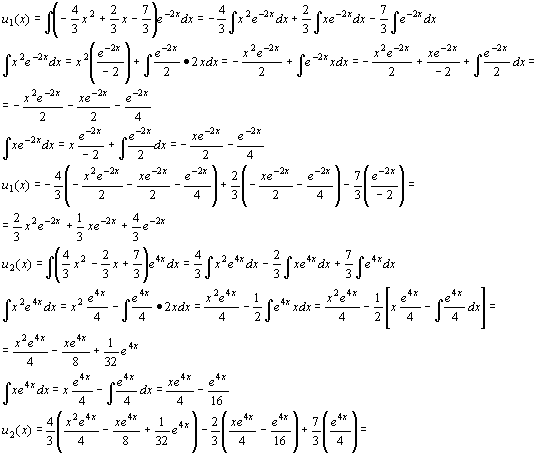
![]()
![]()
Quindi la soluzione generale della non omogenea è:
y(x) = x2 + 2 + C1 e2x + C2 e-4x
I valori di C1 e C2 sono quelli determinati nell’esercizio 1.5.
Esercizio n. 1.21-
Considero 2y’’ + 3y = 0.Allora 2D2 + 3D = 0 che si può scomporre in D(2D+3)=0. Quindi le soluzioni indipendenti sono: u1 (x)=1, u2 (x) = ![]() . Cerchiamo ora una soluzione particolare y1 dell’equazione non omogenea. La funzione 5x + 7 è soluzione dell’ equazione omogenea:
. Cerchiamo ora una soluzione particolare y1 dell’equazione non omogenea. La funzione 5x + 7 è soluzione dell’ equazione omogenea:
D2 y = 0. Perciò se si applica a entrambi i membri dell’equazione non omogenea l’operatore D2 si trova che ogni funzione che soddisfi l’equazione differenziale non omogenea deve anche soddisfare la seguente:
D3 (2D+3) y = 0. Questa equazione differenziale ha le radici caratteristiche 0 di molteplicità 3 e - 3/2. Così tutte le sue soluzioni si trovano nella combinazione lineare y = Ax2 + Bx +C +D![]() dove A,B,C,D sono costanti. Vogliamo scegliere A,B,C,D in modo tale che la soluzione risultante y1 soddisfi l’equazione L(y1 ) = 5x + 7 dove L = D(2D+3). Poichè L(C+D
dove A,B,C,D sono costanti. Vogliamo scegliere A,B,C,D in modo tale che la soluzione risultante y1 soddisfi l’equazione L(y1 ) = 5x + 7 dove L = D(2D+3). Poichè L(C+D![]() ) = 0 per ogni scelta di C, D si debbono soltanto scegliere A e B in modo tale che L(Ax2 + Bx) = 5x + 7 e prendere C = D = 0.
) = 0 per ogni scelta di C, D si debbono soltanto scegliere A e B in modo tale che L(Ax2 + Bx) = 5x + 7 e prendere C = D = 0.
Se si pone y1 = Ax2 + Bx si ha che
D(y1 ) = 2Ax + B e D2 (y1 ) = 2A
Cosi che l’equazione (2D2 + 3D)y = 5x + 7 diventa
2(2A) + 3(2Ax + B) = 5x + 7
dalla quale per identità polinomiale abbiamo il seguente sistema
4A + 3B = 7
6A = 5
con soluzione A= 5/6 e B = 11/9. Allora y1 =![]() e la soluzione generale dell’equazione non omogenea è: y(x) =
e la soluzione generale dell’equazione non omogenea è: y(x) = ![]() + C1 + C2
+ C1 + C2 ![]() .
.
Esercizio n. 1.22-
Il polinomio caratteristico della omogenea è : 2r2 + 3r = 0 che si può scomporre in r(2r + 3) = 0. Quindi le radici sono 0, -3/2. Allora y0 = C1 + C2 ![]() . Ora troviamo una soluzione particolare della non omogenea della forma: yp = u1 y1 +u2 y2 dove y1 , y2 sono soluzioni indipendenti della omogenea. Si considera quindi il seguente sistema:
. Ora troviamo una soluzione particolare della non omogenea della forma: yp = u1 y1 +u2 y2 dove y1 , y2 sono soluzioni indipendenti della omogenea. Si considera quindi il seguente sistema:
u’1 + u’2 ![]() = 0
= 0
![]() u’2
u’2 ![]() =
= ![]()
Il wronskiano è :
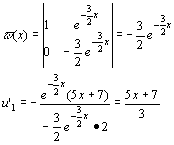
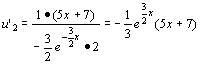
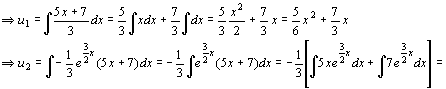
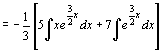
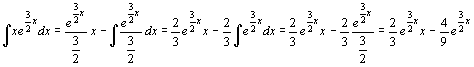
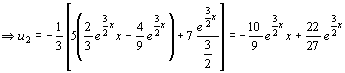
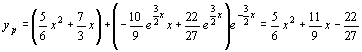
Quindi la soluzione genrale dell’equazione non omogenea è: : y(x) =![]() + C1 + C2
+ C1 + C2 ![]() .
.
Esercizio n. 1.23-
y’’- 4y’ + 4y = 0 Þ r2 -4r + 4 = 0 Þ r1,2 = 2. Cioè abbiamo come radici 2 con molteplicità 2.
y1 = e2x , y2 = xe2x , yp = u1 y1 + u2 y2
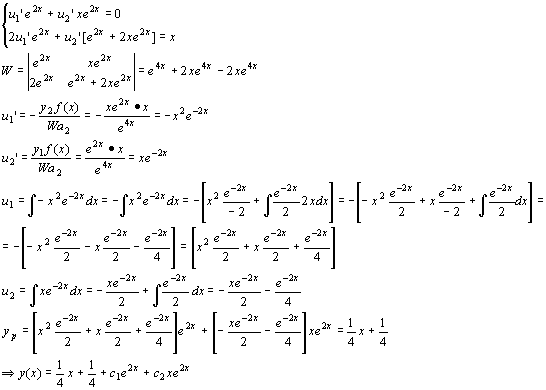
Esercizio n. 1.24-
y’’-3y’ + 2y = 0
r2 - 3r + 2=0
![]()
r1 = 1, r2 = 2
Þ y1 = ex , y2 = e2x, y0 = c1 ex + c2 e2x
![]()
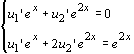
![]()
![]()
![]()
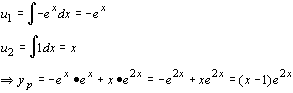
Esercizio n. 1.25-
-2y’’ + y’ = 0 Þ
-2r2 + r = 0Þ
r (-2r + 1 ) = 0 Þ
r1 = 0, r2 = ½ Þ
![]()
![]() , yp = u1 y1 + u2 y2
, yp = u1 y1 + u2 y2
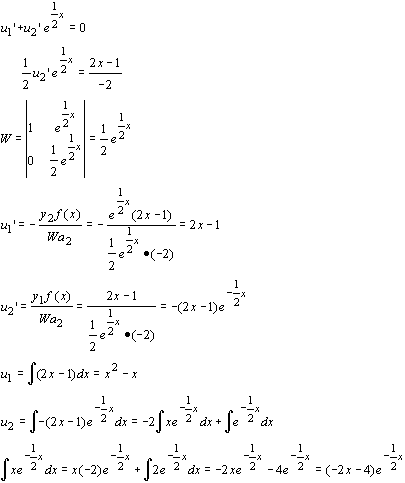
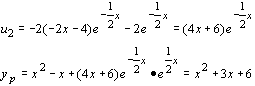
Esercizio n. 1.26-
-2y’’ + y’ = 0 Þ
-2r2 + r = 0 Þ
r(-2r + 1) = 0 Þ
r1 = 0, r2 = ½ Þ
y1 = e0x = 1, y2 = ![]()
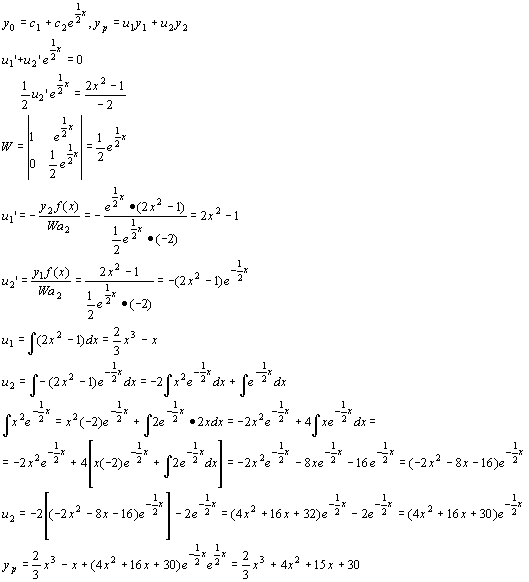
Esercizio n. 1.27-
y’’ - 2y’ + y = 0 Þ r2 -2r + 1 = 0Þ r1,2 = 1Þ y1 = ex, y2 = xex